トーラスで学ぶアニメーションと座標系変換

こんばんは、パイロットの山下ことympbycです。

このブログでは初投稿になります。Pilotでは主にJSの何でも屋をやっています。趣味は高次元幾何学(最近始めた)で、個人ブログは ここ にあります。

今日は回転面トーラスを組み立てながら数式を使ったアニメーションの基本を抑えます。トーラスを使うのは僕がトーラス好きだからです。

z軸が欲しいのでTHREE.jsを使いますが、ライブラリに関係ないエッセンスを抜き出して書いています。2Dアニメーションにも応用できるはずです。

数式で組み立てるアニメーションの基礎

アニメーションフレーム毎に、線形に増加する値に関数を適用して、欲しい動きを作り出すというのが基本です。

例えば、上下にふわふわ揺れるアニメーションはsinを使って、

var y = 0;
function frame () {
    requestAnimationFrame(frame);
    y += 0.1;
    なにか.css({top: Math.sin(x) * 10});
}
requestAnimationFrame(frame);

のようにして実現します。

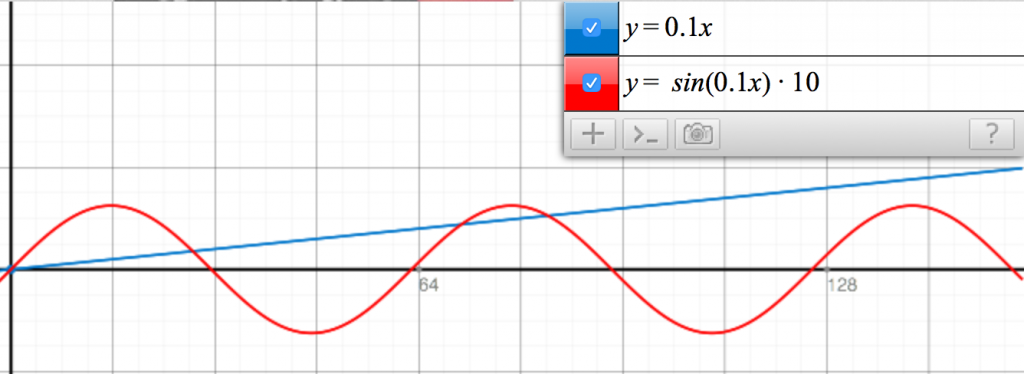
数式を組み立てる時は、http://graph.tk/などを使って、グラフを描くとわかりやすいです。例えば上記の例では、y=0.1xの比例のグラフを、sinに食わせて、結果を10倍しているので、y = sin(0.1x) * 10というグラフになります。このグラフのxを時間に読み替えると、確かに時間が進むにつれて上下に揺れる挙動になっていることがわかると思います。

一番よく使うのはsin, cosで、あとはある時点で急激に値を変化させるのにtanhを使ったり、放物線の動きでy=x^2を使ってみたりします。x軸を時間軸に見立てて欲しい動きをイメージして、それと一致する見た目の関数を探すと楽しいです。

準備

レンダラー、シーン、カメラは適当に作っておきます。

1次元トーラス

0次元トーラスはただの点なので、1次元トーラスからスタートします。

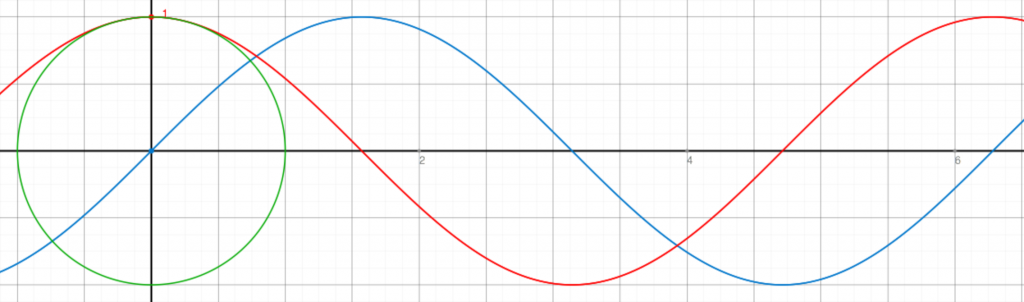
1次元トーラスは円周です。

円の周上の点は半径R(動径)、3時の方向を0とした中心角θ(偏角)で求まります。(R,θ)で表される座標系を円座標系と呼びます。

THREE.jsでは円座標を扱わないので、円座標から3次元直交座標、つまりxyzに変換してやる必要があります。

x: R * cos(θ)
y: R * sin(θ)

コードにするとこう

function circle (r, theta) {
  return new THREE.Vector2(
    r * Math.cos(theta), //x
    r * Math.sin(theta)  //y
  );
}

アニメーションはフレーム毎にθを増やしてやればいいので

var t = 0;
function frame () {
  requestAnimationFrame(frame);
  t += 0.01;
  var c = circle(5, t);
  mesh.position.set(c.x, c.y, 0);
  renderer.render(scene, camera);
}
requestAnimationFrame(frame);

こんな感じになります。

2次元トーラス

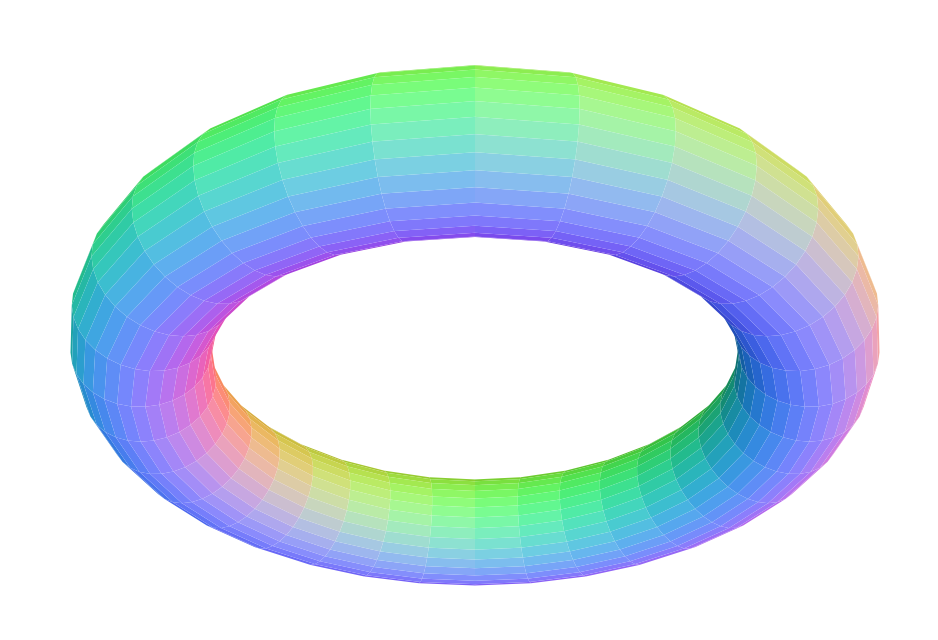
2次元トーラスはドーナツです。

ドーナツ上の座標は、ドーナツの穴の中心から生地の中心までの半径と中心角、生地の半径と中心角の4つの数値(2つの円座標)で決定されます。

これをそれぞれ(R,t,r,p)として、これを3次元直交座標に変換すればTHREE.jsが描画してくれるわけです。

アニメーションとしては、tを線形に増やしていって、pはp=8tで動かすことにします。つまり、ドーナツの生地の表面を螺旋状に渦巻きながらドーナツ自体を周回するようなものになります。

まずはこれをxy平面上に潰したときの動きを作ります。ドーナツをxy平面に潰すとCDのような円盤になります。

tで決定される円周上のxy座標から、pに応じてxとyを増減させてやると

こんな軌道が出来上がります。ここでxとyにそれぞれcos(t)とsin(t)を掛けてやって、tによってxの増減とyの増減が入れ替わるように変化していくことを表現してやれば、

僕らの求めていた星型が出来上がります。あとはz軸方向にp回上下させればいいので、z: r * sin(p)とでもします。

同じことをするのに、ベクトルの演算で円周上の各地点でxy平面自体をz軸について回転してしまうというneatな方法もあります。これについてはまたの機会に書こうと思います。

function disc (R,t,r,p) {
  var c = circle(R,t); //円周上の点
  return new THREE.Vector2(
    c.x + r * Math.cos(p) * Math.cos(t),
    c.y + r * Math.cos(p) * Math.sin(t)
  );
}

function torus (R,t,r,p) {
  var d = disc(R,t,r,p);
  return new THREE.Vector3(
    d.x,
    d.y,
    r * Math.sin(p)
  );
}

僕は数学が苦手でこの計算に丸一日かかったんですが、実はこの式はwikipediaに載っています。
http://ja.wikipedia.org/wiki/トーラス

いい感じっすね。

もしあなたのマシンで描画が重かったらJSFiddleの制約でCanvasRendererを使っているからです。実際に使うときはWebGLRendererを使えばサクサクなはずです。

3次元トーラス and beyond

http://www7b.biglobe.ne.jp/~ykoba/torus3d.html

3次元トーラスは4次元空間にしか描画できないので今回はパスします。断面なら3次元空間に描画できるんですが、座標変換が難しくて…。現在PILOTではn次元空間の座標系アグノスティックな描画エンジンを開発中なので気長にお待ちください。

まとめ

• 円座標系から直交座標系への座標変換を学びました。
• アニメーションを数式から作り出す過程を学びました。
• sin,cosは便利！
• トーラスって面白い！！！！

役に立ったら嬉しいです。

ではではPilotの技術ブログ Mechanic Note を引き続きよろしくお願いします。